Linear Least Squares
Table of Contents:
Due Date
11:59PM, Thursday, September 8, 2022
Introduction
This home work is designed to test your understanding of mathematics tutorial discussed in this link, specifically RANSAC. We highly recommend you to read the entire math tutorial, not just the RANSAC section. The task is to fit the best possible line to two dimensional data points using different linear least square techniques discussed in the tutorials such that the line defines the best possible set of data points:
- Line fitting using Linear Least Squares
- Outliers rejection using Regularization
- Outliers rejection using RANSAC
What you need to do
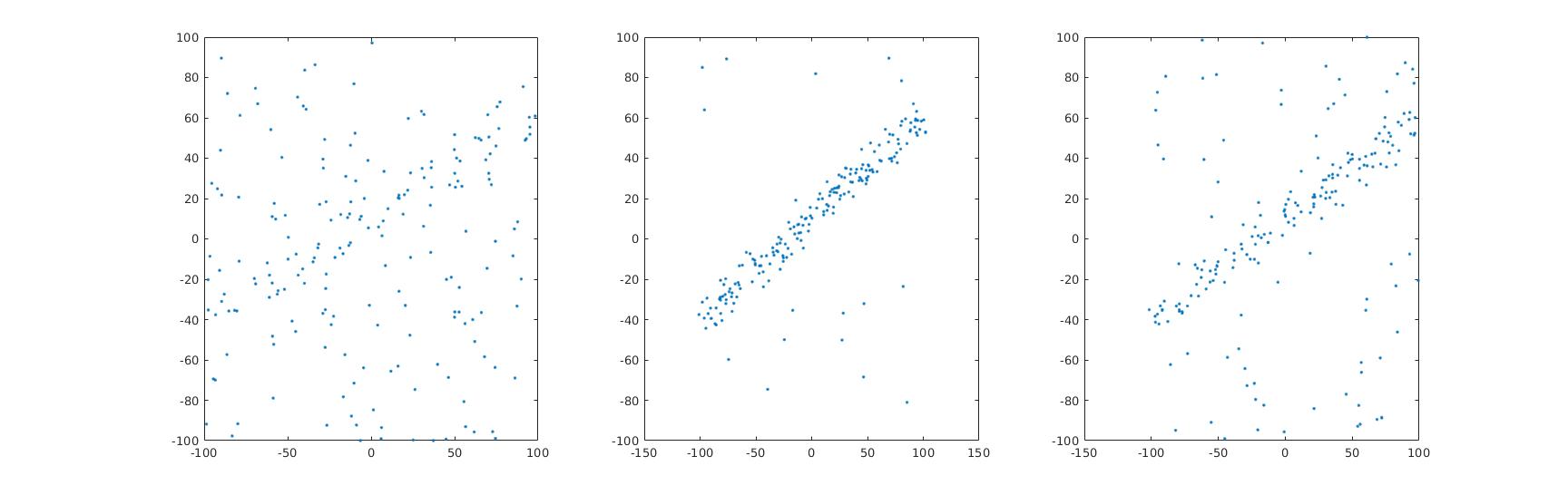
The 2D points data is provided in the form of .mat file (click here to download). The visualization of data with different noise level is shown in the following figure.
Problem Statement
- Write matlab code to visualize geometric interpretation of eigenvalues/covariance matrix as shown in Fig. 10 of this link [40 points]
- Decide the best outlier rejection technique for each of these datasets and write matlab code to fit the line. Also, discuss why your choice of technique is optimal [60 points]
Submission Guidelines
If your submission does not comply with the following guidelines, you’ll be given ZERO credit
File tree and naming
Your submission on Canvas must be a zip file, following the naming convention YourDirectoryID_hw1.zip. For example, xyz123_hw1.zip. The file must have the following directory structure, based on the starter files
YourDirectoryID_hw1.zip.
- data/.
- plot_eigen.m.
- least_square.m.
- report.pdf
Report
For each section of the homework, explain briefly what you did, and describe any interesting problems you encountered and/or solutions you implemented. You must include the following details in your writeup:
- Your understanding of eigenvectors and eigenvalues
- Your choice of outlier rejection technique for each dataset
- Limitation of each outliers rejection technique
Your report must be full English sentences,NOT** commented code. There is a word limit of 750 words and no minimum length requirement**
Collaboration Policy
You are encouraged to discuss the ideas with your peers. However, the code should be your own, and should be the result of you exercising your own understanding of it. If you reference anyone else’s code in writing your project, you must properly cite it in your code (in comments) and your writeup. For the full honor code refer to the CMSC426 website