Table of Contents:

Deadline

11:59:59PM, Tuesday, December 16, 2019

  • This is a strict deadline– we will not accept late submissions, with of without late days. Submissions made by 11:59PM December 10 will receive extra credit equal to 20% of their grade on the project.

Introduction

Factor graphs are graphical models that are well suited to modeling complex estimation problems such as Simultaneous Localization and Mapping (SLAM) or Structure from Motion (SfM). You might be familiar with another often used graphical model, Bayesian Networks [1]. Unlike Bayesian Networks, which are directed acyclic graphs (DAG), factor graphs are bipartite graphs consisting of factors connected to variables. Variables represent the unknown random variables and factors represent probabilistic information on those variables, derived from measurement or prior knowledge.

In this project, you’ll implement a Bayesian Network-based solution to SLAM, an estimation problem that’s ubiquitous in robotics. You’ll first familiarize yourself with the algorithm in a simplified setting, before diving into the full problem. Both our “toy problem” and your project are based on the GTSAM[2] (“Georgia Tech Smoothing and Mapping”) toolbox which can be downloaded from this link.

It’s surprising how effectively the factor graph-based frameworks can solve a problem as complex as SLAM (where they provide state-of-the-art performance). Excited already?

For more details about the homework refer to the relevant course notes.

Part 1: Intro to GTSAM

To help you familiarize yourself with GTSAM and its application to SLAM, we’ve implemented a “toy example” application. Find it here. We highly recommend that you install and run it, and gain an understanding of how the code works, before moving on to the rest of the project.

Part 2: SLAM Implementation

Now that you’re familiar with how GTSAM can be applied to SLAM in the 2D setting, you’re ready to implement it yourself– in 3D!

We’ve recorded some videos from the perspective of a small drone. Your task is to build a map based on the observation measurements the drone makes.
You’ll use data from the DataMapping.mat file to build a map and localize your robot on the map (Simultaneous Localization and Mapping) using the GTSAM package.

The Environment

The provided data for this phase was collected with a hand-held SLAMDunk sensor module [3] (shown in Fig. 1), manufactured by Parrot R , simulating flight patterns over a floor mat of AprilTags [4] each of which has a unique ID.

Figure 1: Parrot SLAMDunk

The data contains the rectified left camera images, IMU data, SLAMDunk’s pose estimates, AprilTag [4] detections with tag size and camera intrinsics and extrinsics. All units are in m, rad, rads^1 and ms^2 if not specified.

Camera Intrinsics and Extrinsics are given specifically in CalibParams.mat and has the following parameters:

  • K has the camera intrinsics (assume that the distortion coefficients in the radtan model are zero).
  • TagSize is in size of each AprilTag in meters.
  • qIMUToC has the quaternion to transform from IMU to Camera frame (QuaternionW, QuaternionX, QuaternionY, QuaternionZ).
  • TIMUToC has the translation to transform from IMU to Camera frame (TransX, TransY, TransZ).

The .mat file for any of the sequence (in the format DataNAME OF SEQUENCE.mat for e.g., DataSquare.mat where Square is the sequence name) will contain the following data:

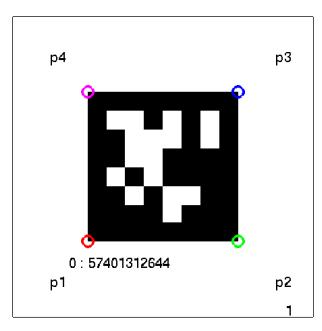
  • DetAll is a cell array with AprilTag detections per frame. For e.g., frame 1 detections can be extracted as DetAll{1}. Each cell has multiple rows of data. Each row has the following data format:
    • [TagID, p1x, p1y, p2x, p2y, p3x, p3y, p4x, p4y]
      • Here p1 is the left bottom corner and points are incremented in counter-clockwise direction, i.e., the p1x, p1y are coordinates of the bottom left, p2 is bottom right, p3 is top right, and p4 is top left corners (Refer to Fig. 2). You will use the left bottom corner (p1) of Tag 10 as the world frame origin with positive X being direction pointing from p1 to p2 in Tag 10 and positive Y being pointing from p1 to p4 in Tag 10 and Z axis being pointing out of the plane (upwards) from the Tag.
    • IMU is a cell array where each row has the following data:
      • [QuaternionW, QuaternionX, QuaternionY, QuaternionZ, AccelX, AccelY, AccelZ, GyroX, GyroY, GyroZ, Timestamp]
      • You do not need the IMU readings for this project, however, if you find a creative way to use it, please feel free to use it.
    • LeftImgs is a cell array where each cell is a Image.
    • TLeftImgs is the Timestamps for LeftImgs. For e.g. LeftImgs{1} was collected at time TLeftImgs(1).
    • Pose is an array with each row in the form:
      • [PosX, PosY, PosZ, QuaternionW, QuaternionX, QuaternionY, QuaternionZ, EulerX, EulerY, EulerZ, Timestamp]
      • Here ZYX Euler angle was used which is the default for Matlab’s quat2eul function.
Figure 2: AprilTag, with corners highlighted.

Implementation Overview

Download the starter code and data here

Code

The starter code can be found in the code folder. There are two .m files in the folder: SLAMUsingGTSAM.m and Wrapper.m. Your SLAM implementation goes in SLAMUsingGTSAM (you may also use helper functions in additional files). The script Wrapper.m is given for your debugging only. The input and output for the SLAMUsingGTSAM are given in the “Environment” section above. The SLAMUsingGTSAM function has two return arguments, LandMarksComputed and AllPosesComputed:

  • LandMarksComputed is an array of landmark locations.
    • Each row is of the form [TagID, p1x, p1y, p2x, p2y, p3x, p3y, p4x, p4y].
    • Note that the rows have to be sorted in ascending order by TagIDs.
  • AllPosesComputed is an array of 6DOF poses.
    • Each row gives the pose measurement at a single camera timestep.
    • Each row is of the form [PosX, PosY, PosZ, Quaternion, QuaternionX, QuaternionY, QuaternionZ].
      • (We use quaternions because euler angles flip near singularity conditions– similar to the ones we are operating in.)

Please note:

  • Do NOT add any subdirectories.
  • Comment out any visualization code or debug print statements before submitting.

Submission Guidelines

We will deduct points if your submission does not comply with the following guidelines.

Please submit the project once for your group – there’s no need for each member to submit it.

File tree and naming

Your submission on Canvas must be a zip file, following the naming convention YourDirectoryID_proj4.zip. For example, xyz123_proj4.zip. The file must have the following directory structure:

  • YourDirectoryID_proj4.zip/
    • code/
      • SLAMusingGTSAM.m
      • *(any dependencies of SLAMusingGTSAM.m)
    • report.pdf

Report

You will be graded primarily based on your report.

Logistics and bookkeeping you must include at the top of your report:

  • The name of each group member.
  • A brief (one paragraph or less) description of what each group member contributed to the project.

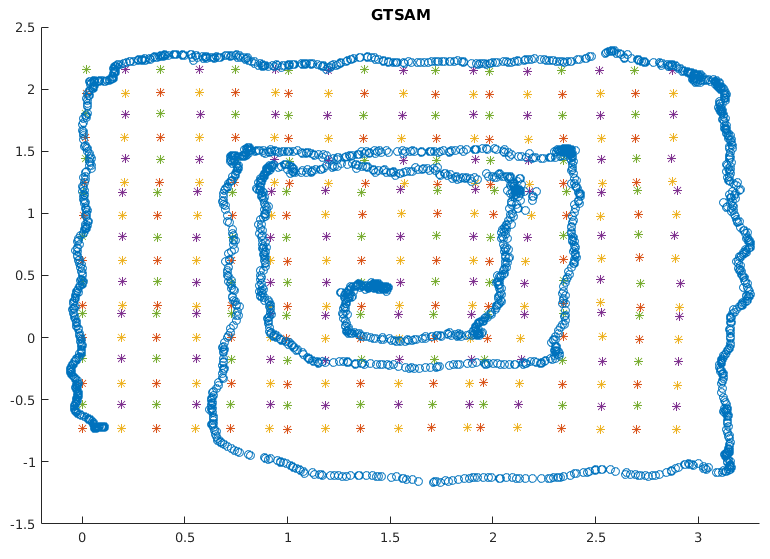
You must include output plots of the landmarks in 3D with the camera poses/localization, as shown in the example below.

Plot of landmark and camera poses, viewed from above. Please also provide plots viewed from the side.

We want you to demonstrate an understanding of the concepts involved in the project, and to show the output produced by your code.

Assume that we’re familiar with the project, so you don’t need to spend time repeating what’s already in the course notes. Instead, focus on any interesting problems you encountered and/or solutions you implemented.

As usual, your report must be full English sentences, not commented code. There is a word limit of 1500 words and no minimum length requirement.

Collaboration Policy

We encourage you to work closely with your groupmates, including collaborating on writing code. With students outside your group, you may discuss methods and ideas but may not share code.

For the full collaboration policy, including guidelines on citations and limitations on using online resources, see the course website.

References:

[1] Bernd Pfrommer, Nitin Sanket, Kostas Daniilidis, and Jonas Cleveland. Penncosyvio: A challenging visual inertial odometry benchmark. In 2017 IEEE International Conference on Robotics and Automation (ICRA), pages 3847–3854, May 2017.

[2] Michael Bloesch, Michael Burri, Sammy Omari, Marco Hutter, and Roland Siegwart. Iterated extended kalman filter based visual-inertial odometry using direct photometric feedback. The International Journal of Robotics Research, 36(10):1053–1072, 2017.

[3] Parrot. SLAMDunk. http://developer.parrot.com/docs/slamdunk/, 2016.

[4] Edwin Olson. AprilTag: A robust and flexible visual fiducial system. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), pages 3400–3407. IEEE, May 2011.